فيديو: لماذا من المهم النظر في التعددية عند تحديد جذور معادلة كثيرة الحدود؟
2024 مؤلف: Miles Stephen | [email protected]. آخر تعديل: 2023-12-15 23:33
على سبيل المثال ، عدد المرات المعطى معادلة كثيرة الحدود لديه جذر في نقطة معينة هو تعدد من ذلك جذر . مفهوم تعدد يكون الأهمية لتتمكن من العد بشكل صحيح دون تحديد استثناءات (على سبيل المثال ، double الجذور عد مرتين). ومن هنا جاءت عبارة "عد بـ تعدد ".
إذن ، لماذا الجذور متعددة الحدود مهمة؟
العثور على الجذور من أ متعدد الحدود للغاية الأهمية تعمل في الرياضيات التطبيقية لأن العديد من المسائل تحتاج إلى معادلة تفاضلية خطية عادية ليتم حلها (على سبيل المثال: مذبذب توافقي ، دائرة كهربائية LRC ، …).
بعد ذلك ، السؤال هو كيف تحدد التعددية؟ كم مرة يكون رقم معين صفرًا لكثير حدود معين. على سبيل المثال ، في دالة كثيرة الحدود f (x) = (x – 3) 4 (x –5) (x –8) 2 ، يكون للصفر 3 تعدد 4 ، 5 has تعدد 1 و 8 has تعدد 2. بالرغم من أن كثير الحدود هذا لا يحتوي إلا على ثلاثة أصفار ، إلا أننا نقول إن بها عد سبعة أصفار تعدد.
في هذا الصدد ، كيف تعمل المضاعفات؟
يتكرر العامل ، أي أن العامل (x − 2) يظهر مرتين. عدد المرات التي يظهر فيها عامل معين في الشكل المحلل إلى عوامل من معادلة كثير الحدود يسمى تعدد . الصفر المرتبط بهذا العامل ، x = 2 ، له تعدد 2 لأن العامل (x − 2) يحدث مرتين.
كيف ترسم دالة كثيرة الحدود؟
- الخطوة 1: تحديد سلوك نهاية الرسم البياني.
- الخطوة 2: ابحث عن تقاطعات x أو أصفار الوظيفة.
- الخطوة 3: ابحث عن تقاطع y للدالة.
- الخطوة 4: تحديد ما إذا كان هناك أي تناظر.
- الخطوة 5: ابحث عن عدد نقاط التحول القصوى.
- الخطوة 6: ابحث عن نقاط إضافية ، إذا لزم الأمر.
- الخطوة 7: ارسم الرسم البياني.
موصى به:
ما هو حثل قصر النظر؟
الحثل العضلي هو اضطراب وراثي طويل الأمد يؤثر على وظيفة العضلات. تشمل الأعراض التدهور التدريجي لفقدان العضلات وضعفها. غالبًا ما تنقبض العضلات وتكون غير قادرة على الاسترخاء. قد تشمل الأعراض الأخرى إعتام عدسة العين والإعاقة الذهنية ومشاكل توصيل القلب
لماذا يتفوق نظام جاليليو على نظام تحديد المواقع العالمي (GPS) عند اكتماله وتشغيله؟
تم تصميم GPS واستخدم لأول مرة للتطبيقات العسكرية. لماذا يتفوق نظام جاليليو على نظام تحديد المواقع العالمي (GPS) عند اكتماله وتشغيله؟ سوف يتفوق نظام جاليليو على نظام تحديد المواقع العالمي (GPS) في المقام الأول بسبب دقة تقنية الساعة الخاصة به
لماذا تسمى كثيرة الحدود من الدرجة الثانية تربيعية؟
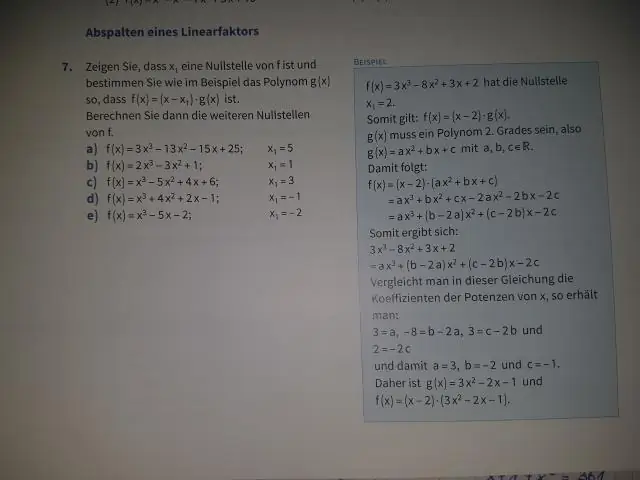
هذه هي الحالة لأن الكلمة quadratum هي الكلمة اللاتينية للمربع ، وبما أن مساحة مربع طول الضلع x تُعطى بواسطة x2 ، تُعرف المعادلة متعددة الحدود التي تحتوي على الأس اثنين بالمعادلة التربيعية ("التربيعية"). بالامتداد ، السطح التربيعي هو سطح جبري من الدرجة الثانية
ما هي الحدود المتقاربة المتباعدة وتحول الحدود؟
تمثل الحدود المتقاربة والمتباعدة والمتحولة المناطق التي تتفاعل فيها الصفائح التكتونية للأرض مع بعضها البعض. تحدث الحدود المتقاربة ، التي توجد منها ثلاثة أنواع ، حيث تتصادم الصفائح. تحدث حدود التحويل حيث تنزلق الألواح فوق بعضها البعض
ما هو السلوك النهائي لدالة كثيرة الحدود برينلي؟
رسم بياني مع النهاية اليسرى لأسفل والنهاية اليمنى لأعلى. المعامل الرئيسي سالب ثم الأيسر لأعلى والطرف الأيمن لأسفل. لذلك ، دالة كثيرة الحدود لها درجة فردية والمعامل الرئيسي سالب