
- مؤلف Miles Stephen stephen@answers-science.com.
- Public 2023-12-15 23:33.
- آخر تعديل 2025-01-22 16:55.
الوظيفة قابل للتفاضل عند نقطة ما إذا كان ظل الخط عرضي هناك. في المقابل ، عمودي ظل توجد خطوط حيث يكون ميل الوظيفة غير محدد. الوظيفة ليست كذلك قابل للتفاضل عند نقطة ما إذا كان ظل الخط عمودي هناك.
وبالمثل ، هل الرسم البياني قابل للاشتقاق عند المماس الأفقي؟
حيث f (x) لها أ ظل أفقي خط ، f '(x) = 0. إذا كانت الوظيفة قابل للتفاضل عند نقطة ما ، فهو مستمر عند هذه النقطة. وظيفة ليست كذلك قابل للتفاضل عند نقطة ما إذا لم تكن متصلة عند النقطة ، إذا كان لها عمودي ظل عند النقطة ، أو إذا كان رسم بياني له زاوية حادة أو نتوء.
ثانيًا ، عندما يكون خط الظل عموديًا؟ أ ظل منحنى هو أ خط التي تلامس المنحنى عند نقطة واحدة. له نفس ميل المنحنى عند تلك النقطة. أ الظل العمودي يلامس المنحنى عند نقطة يكون فيها الانحدار (ميل) المنحنى لانهائيًا وغير محدد. على الرسم البياني ، يتم تشغيله بالتوازي مع المحور ص.
علاوة على ذلك ، هل الظل الرأسي قابل للتفاضل؟
في الرياضيات ، وخاصة حساب التفاضل والتكامل ، أ الظل العمودي هو ظل خط ذلك عمودي . لأن أ عمودي الخط له منحدر لانهائي ، دالة لها الرسم البياني أ الظل العمودي ليس قابل للتفاضل عند نقطة التماس.
ما الذي يجعل الشيء مميزًا؟
وظيفة يكون قابل للتفاضل في نقطة عندما يكون هناك مشتق محدد في تلك المرحلة. هذا يعني أن ميل خط المماس للنقاط من اليسار يقترب من نفس قيمة ميل مماس النقاط من اليمين.
موصى به:
كيف تجد الامتداد الأفقي؟

إذا كانت b> 1 ، فإن الرسم البياني يمتد بالنسبة لمحور y ، أو رأسياً. إذا كان b <1 ، يتقلص الرسم البياني بالنسبة لمحور y. بشكل عام ، يتم إعطاء الامتداد الأفقي بواسطة المعادلة y = f (cx) y = f (c x)
ما هو الفرق بين الرسم البياني الشريطي الأفقي والرأسي؟
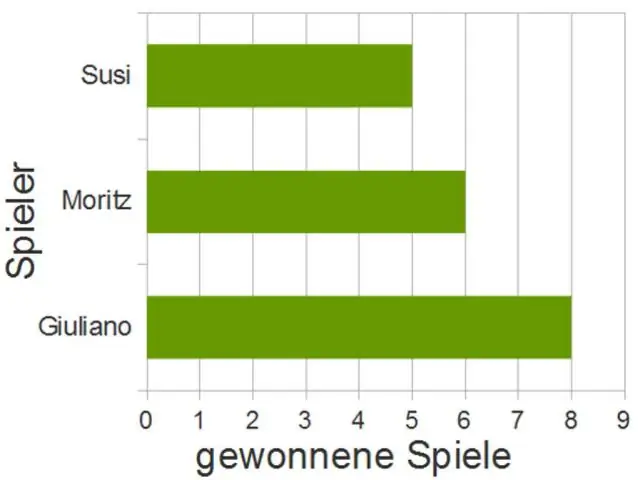
يخبر عنوان الرسم البياني الشريطي الأفقي عن البيانات التي يمثلها الرسم البياني. يمثل المحور الرأسي فئات البيانات. هنا ، فئات البيانات هي الألوان. يمثل المحور الأفقي القيم المقابلة لكل قيمة بيانات
هل أكسيد النيكل قابل للذوبان أم غير قابل للذوبان؟

أكسيد النيكل قابل للذوبان في الأحماض وسيانيد البوتاسيوم وهيدروكسيد الأمونيوم. إنه غير قابل للذوبان في كل من الماء البارد والساخن ، والمحاليل الكاوية. الشكل الأسود لأكسيد النيكل متفاعل كيميائيًا ، في حين أن شكل أكسيد النيكل الأخضر خامل ومقاوم للصهر
كيف تجد معادلة خط المماس للمشتق؟

1) أوجد المشتق الأول لـ f (x). 2) عوض xvalue من النقطة المشار إليها في f '(x) لإيجاد الميل عند x. 3) عوّض بقيمة x في f (x) لإيجاد إحداثي y لنقطة الظل. 4) اجمع المنحدر من الخطوة 2 والنقطة من الخطوة 3 باستخدام صيغة نقطة الميل لإيجاد معادلة خط الظل
كيف تجد خط المماس الأفقي؟

ميل الخطوط الأفقية يساوي صفر. لذلك ، عندما تكون المشتقة صفرًا ، يكون خط المماس أفقيًا. لإيجاد خطوط المماس الأفقية ، استخدم مشتق الدالة لتحديد موقع الأصفار وعوضهم مرة أخرى في المعادلة الأصلية
