جدول المحتويات:
فيديو: ما هو في الإحصاء؟
2024 مؤلف: Miles Stephen | [email protected]. آخر تعديل: 2023-12-15 23:33
الرمز ' σ يمثل "الانحراف المعياري للمجتمع. المصطلح "sqrt" المستخدم في هذا إحصائية الصيغة تدل على الجذر التربيعي. المصطلح ' Σ (Xأنا - Μ)2'المستخدمة في إحصائية تمثل الصيغة مجموع الانحرافات التربيعية للنتائج من وسط السكان.
فيما يتعلق بهذا ، ماذا تعني σ؟
Σ هذا الرمز (يسمى سيجما) يعني "تلخيص" أنا أحب سيجما ، إنه ممتع للاستخدام ، ويمكن فعل أشياء ذكية كثيرة.
بالإضافة إلى ذلك ، ماذا تعني U في الإحصائيات؟ يو (أ ، ب) توزيع موحد. احتمالية متساوية في النطاق أ ، ب.
وبالمثل ، قد تسأل ، ما هي الرموز في الإحصاء؟
عرض أو طباعة: تتغير هذه الصفحات تلقائيًا لشاشتك أو طابعتك.
| عينة إحصائية | المعلمة السكان | وصف |
|---|---|---|
| x¯ "x-bar" | Μ "mu" أو Μx | يقصد |
| M أو Med أو x ~ "x-tilde" | (لا أحد) | الوسيط |
| s (TIs تقول Sx) | σ "سيجما" أو σx | الانحراف المعياري للتباين ، قم بتطبيق رمز مربع (s² أو σ²). |
| ص | ρ "رو" | معامل الارتباط الخطي |
كيف تحسب الانحراف المعياري؟
لحساب الانحراف المعياري لتلك الأرقام:
- احسب المتوسط (المتوسط البسيط للأرقام)
- ثم لكل رقم: اطرح المتوسط وربّع النتيجة.
- ثم احسب متوسط تلك الفروق التربيعية.
- خذ الجذر التربيعي لذلك وانتهينا!
موصى به:
ما هي مجالات الإحصاء؟
سنناقش الآن بعض المجالات المهمة التي يتم فيها تطبيق الإحصاء بشكل شائع. (1) الأعمال. (2) الاقتصاد. (3) الرياضيات. (4) البنوك. (5) إدارة الدولة (الإدارة) (6) المحاسبة والتدقيق. (7) العلوم الطبيعية والاجتماعية. (8) علم الفلك
ما هي النسبة في الإحصاء؟
بيانات النسبة: التعريف. يتم تعريف بيانات النسبة على أنها بيانات كمية ، لها نفس خصائص بيانات الفاصل الزمني ، مع نسبة متساوية ونهائية بين كل بيانات و "الصفر" المطلق يتم التعامل معها كنقطة أصل
ما هي مقاييس القياس في الإحصاء؟
تستخدم مقاييس القياس لتصنيف و / أو تحديد المتغيرات. يصف هذا الدرس المقاييس الأربعة المستخدمة بشكل شائع في التحليل الإحصائي: المقاييس الاسمية والترتيبية والفاصلة والنسبة
ماذا يعني شي في الإحصاء؟
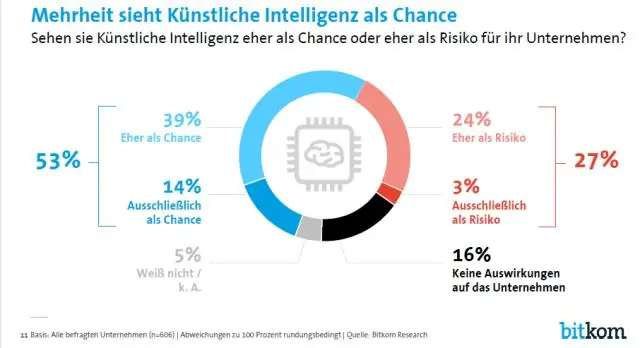
تمثل xi قيمة i للمتغير X. بالنسبة للبيانات ، x1 = 21 ، x2 = 42 ، وهكذا. • الرمز & سيجما. ("العاصمة سيجما") تشير إلى وظيفة الجمع
ما معنى الاختلاف في الإحصاء؟
ما هو التباين في الإحصاء؟ يشير التغير (ويسمى أيضًا الانتشار أو التشتت) إلى مدى انتشار مجموعة من البيانات. يمنحك المتغير طريقة لوصف مدى اختلاف مجموعات البيانات ويسمح لك باستخدام الإحصائيات لمقارنة بياناتك بمجموعات أخرى من البيانات